解題程式碼

var pathSum = function (root, targetSum) {
  if (!root) return 0;
  let paths = 0;
  const nodeMap = new Map();

  const DFS = (node, curSum) => {
    if (curSum === targetSum) paths++;
    if (nodeMap.has(curSum - targetSum)) paths += nodeMap.get(curSum - targetSum);
    nodeMap.set(curSum, (nodeMap.get(curSum) || 0) + 1);

    if (node.left) DFS(node.left, curSum + node.left.val);
    if (node.right) DFS(node.right, curSum + node.right.val);

    nodeMap.set(curSum, nodeMap.get(curSum) - 1);
  };
  DFS(root, root.val);

  return paths;
};

解題思路、演算法

這題可以使用 DFS + HashMap 來解題。首先用 DFS 搜尋二元樹的各個路徑，並同時將經過路徑的所有節點總和記錄在 HashMap。

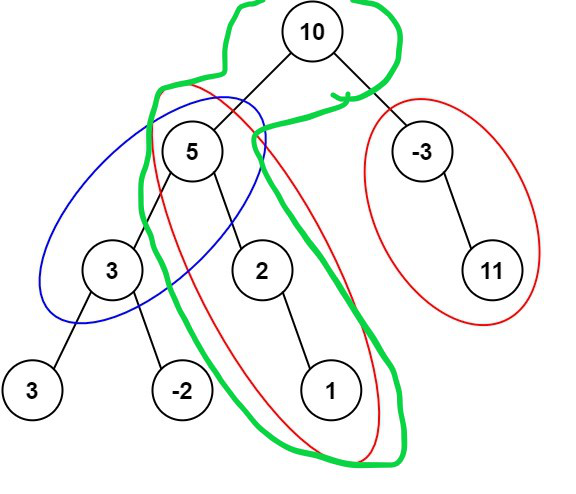
例如當前走過了 10 => 5 => 2 => 1 的路徑(綠色線圈起的部分)，hashMap 會有以下鍵值對

{ 10: 1, 15: 1, 17: 1, 18: 1}

此時拿 18 - 8(targetSum) = 10，10 存在於 HashMap 中，就可以知道在這條路徑下有一段路的節點總和為 targetSum，這種是從樹的中間層開始總和為 targetSum 的情況，而另一種 case 是從根節點的總和等於 targetSum 的情況，

有點像是以前遇過的 prefix sum 的概念

而為了避免會重複計算到路徑，當搜尋完回到二元樹的上層節點時，要記得把 hashMap 中的路徑減掉，例如搜尋完回到節點 2，減掉 key 為 18 的路徑一次，回到節點 5，減掉 key 為 17 的路徑一次。

case 範例: root = [1,-2,-3]，targetSum = -1

解法的時間、空間複雜度

時間複雜度: O(n)
空間複雜度: O(n)

參考資料

Path Sum III | Leet code 437 | Theory explained + Python code

贾考博 LeetCode 437. Path Sum III